ریاضی علم شگفتی ها

1 x 8 + 1 = 9
12 x 8 + 2 =98
123 x8 + 3 = 987
1234 x 8 + 4 = 9876
12345 x 8 + 5 = 98765
123456 x 8 + 6 = 987654
1234567 x 8 + 7 = 9876543
12345678 x 8 + 8 = 98765432
123456789 x 8 + 9 = 987654321

1 x 9 + 2 = 11
12 x 9 + 3 = 111
123 x 9 + 4 = 1111
1234 x 9 + 5 = 11111
12345 x 9 + 6 = 111111
123456 x 9 + 7 = 1111111
1234567 x 9 + 8 = 11111111
12345678 x 9 + 9 = 111111111
123456789 x 9 +10 = 1111111111
9 x 9 + 7 = 88
98 x 9 + 6 = 888
987 x 9 + 5 = 8888
9876 x 9 + 4 = 88888
98765 x 9 + 3 = 888888
987654 x 9 + 2 = 8888888
9876543 x 9 + 1 = 88888888
98765432 x 9 + 0 = 888888888

1 x 1 = 1
11 x 11 = 121
111 x 111 = 12321
1111 x 1111 = 1234321
11111 x 11111 = 123454321
111111 x 111111 = 12345654321
1111111 x 1111111 = 1234567654321
11111111 x 11111111 = 123456787654321
111111111 x 111111111 = 12345678987654321

روزی دو دوست، یک مهندس و یک فیزیکدان سوار بالون شدند. پس از مدتی فهمیدند که بالون، آنها را به صحرایی دوردست برده است. آنها گم شده بودند. هردو با هم شروع به فریاد زدن کردند: "آهـــــــــــــــــــــای! ما کجـــا هستیــــــــم"؟
این کار را چند بار تکرار کردند و بعد خسته و ناامید نشستند.
ده دقیقه بعد صدایی شنیدند که می گفت: "اوهـــوی! شما داخل یک بالون هستیــــد".
مهندس گفت: "شرط می بندم که این صدا، صدای یک ریاضی دان است".
فیزیکدان پرسید: "از کجا اینقدر مطمئن هستی"؟
مهندس گفت: "چون جوابی که به سوال ما داده صد درصد درست و مطلقا بدردنخور بود" !

این شعر رو حمید برامون فرستاده دستشون درد نکنه............

رابطه عشق و معدن یا ریاضیات و معدن رو در آینده خواهیم داشت .

*شعری از پروفسور هشترودی در مورد ریاضیات*



*منحنی قامتم، قامت ابروی توست
خط مجانب بر آن، سلسله گیسوی توست

بی تو وجودم بود یک سری واگرا
ناحیه همگراش دایره روی توست

کار بررسی  مقالات و فایل های کارگاه و نمایشگاه از روز چهارشنبه 15/2/89 آغاز گردیده است. نتایج داوری و پذیرش مطابق فراخوان شماره 2 در سایت کنفرانس اعلام می گردد.

جهت دیدن سایز بزرگ تصاویر بر روی تصویر مورد نظر کلیک نمایید
تصویر فراخوان
روی فراخوان	پشت فراخوان
روی فراخوان	پشت فراخوان

تصویر پوستر

انسان اولیه نسبت به اعداد بیگانه بود و شمارش اشیاء اطراف خود را به حسب غریزه یعنی همانطور که مثلاً مرغ خانگی تعداد جوجه هایش را می داند انجام می داد اما به زودی مجبور شد وسیله شمارش دقیق تری بوجود آورد لذا به کمک انگشتان دست دستگاه شماری پدید آورد که مبنای آن 60 بود.
این دستگاه شمار که بسیار پیچیده می باشد قدیمی ترین دستگاه شماری است که آثاری از آن در کهن ترین مدارک موجود یعنی نوشته های سومری مشاهده می شود. سومریها که تمدنشان مربوط به حدود هزار سال قبل از میلاد مسیح است در جنوب بین النهرین یعنی ناحیه بین دو رود دجله و فرات ساکن بودند. آنها در حدود 2500 سال قبل از میلاد با امپراطوری سامی عکاد متحد شدند و امپراطوری و تمدن آشوری را پدید آوردند.
نخستین دانشمند معروف یونانی طالس ملطلی (639- 548 ق. م.) است که در پیدایش علوم نقش مهمی به عهده داشت و می توان وی را موجد علوم فیزیک، نجوم و هندسه دانست. در اوایل قرن ششم ق. م. فیثاغورث (572-500 ق. م.) از اهالی ساموس یونان کم کم ریاضیات را بر پایه و اساسی قرار داد و به ایجاد مکتب فلسفی خویش همت گماشت. پس از فیثاغورث باید از زنون فیلسوف و ریاضیدان یونانی که در 490 ق. م. در ایلیا متولد شده است نام ببریم. در اوایل نیمه دوم قرن پنجم بقراط از اهالی کیوس قضایای متفرق آن زمان را گردآوری کرد و در حقیقت همین قضایا است که مبانی هندسه جدید ما را تشکیل می دهند.
در قرن چهارم قبل از میلاد افلاطون در باغ آکادموس در آتن مکتبی ایجاد کرد که نه قرن بعد از او نیز همچنان برپا ماند. این فیلسوف بزرگ به تکمیل منطق که رکن اساسی ریاضیات است همت گماشت و چندی بعد منجم و ریاضی دان معاصر وی ادوکس با ایجاد تئوری نسبتها نشان داد که کمیات اندازه نگرفتنی که تا آن زمان در مسیر علوم ریاضی گودالی حفر کرده بود هیچ چیز غیرعادی ندارد و می توان مانند سایر اعداد قواعد حساب را در مورد آنها به کار برد.
در قرن دوم ق. م. نام تنها ریاضی دانی که بیش از همه تجلی داشت ابرخس یا هیپارک بود. این ریاضیدان و منجم بزرگ گامهای بلند و استادانه ای در علم نجوم برداشت و مثلثات را نیز اختراع کرد. بطلمیوس که به احتمال قوی با امپراطوران بطالسه هیچگونه ارتباطی ندارد در تعقیب افکار هیپارک بسیار کوشید. در سال 622 م. که حضرت محمد (ص) از مکه هجرت نمود در واقع آغاز شکفتگی تمدن اسلام بود.
در زمان مأمون خلیفه عباسی تمدن اسلام به حد اعتلای خود رسید به طوری که از اواسط قرن هشتم تا اواخر قرن یازدهم زبان عربی زبان علمی بین المللی شد. از ریاضیدانان بزرگ اسلامی این دوره یکی خوارزمی می باشد که در سال 820 به هنگام خلافت مأمون در بغداد کتاب مشهور الجبر و المقابله را نوشت.
دیگر ابوالوفا (998-938) است که جداول مثلثاتی ذیقیمتی پدید آورد و بالاخره محمد بن هیثم (1039-965) معروف به الحسن را باید نام برد که صاحب تألیفات بسیاری در ریاضیات و نجوم است. قرون وسطی از قرن پنجم تا قرن دوازدهم یکی از دردناکترین ادوار تاریخی اروپاست. عامه مردم در منتهای فلاکت و بدبختی به سر می بردند. برجسته ترین نامهایی که در این دوره ملاحظه می نماییم در مرحله اول لئونارد بوناکسی (1220-1170) ریاضیدان ایتالیایی است. دیگر نیکلاارسم فرانسوی می باشد که باید او را پیش قدم هندسه تحلیلی دانست.
در قرون پانزدهم و شانزدهم دانشمندان ایتالیایی و شاگردان آلمانی آنها در حساب عددی جبر و مکانیک ترقیات شایان نمودند. در اواخر قرن شانزدهم در فرانسه شخصی به نام فرانسوا ویت (1603-1540م) به پیشرفت علوم ریاضی خدمات ارزنده‌ای نمود. وی یکی از واضعین بزرگ علم جبر و مقابله جدید و در عین حال هندسه دان قابلی بود.
? کوپرنیک (1543-1473) منجم بزرگ لهستانی در اواسط قرن شانزدهم درکتاب مشهور خود به نام درباره دوران اجسام آسمانی منظومه شمسی را این چنین ارائه داد:
1) مرکز منظومه شمسی خورشید است نه زمین.
2) در حالیکه ماه به گرد زمین می چرخد سیارات دیگر همراه با خود زمین به گرد خورشید می چرخند.
3) زمین در هر 24 ساعت یکبار حول محور خود می چرخد، نه کره ستاره های ثابت.
پس از مرگ کوپرنیک مردی به نام تیکوبراهه در کشور دانمارک متولد شد. وی نشان داد که حرکت سیارات کاملاً با نمایش و تصویر دایره های هم مرکز وفق نمی دهد. تجزیه و تحلیل نتایج نظریه تیکوبراهه به یوهان کپلر که در سال آخر زندگی براهه دستیار وی بود محول گشت. پس از سالها کار وی به نخستین کشف مهم خود رسید و چنین یافت که سیارات در حرکت خود به گرد خورشید یک مدار کاملاً دایره شکل را نمی پیمایند بلکه همه آنها بر روی مدار بیضی شکل حرکت می کنند که خورشید نیز در یکی از دو کانون آنها قرار دارد. قرن هفدهم در تاریخ ریاضیات قرنی عجیب و معجزه آساست.
از فعالترین دانشمندان این قرن کشیشی پاریسی به نام مارن مرسن که می توان وی را گرانبها ترین قاصد علمی جهان دانست. در سال 1609 گالیله ریاضیات و نجوم را در دانشگاه پادوا در ایتالیا تدریس می کرد. وی یکی از واضعین مکتب تجربی است. وی قانون سقوط اجسام را به دست آورد و مفهوم شتاب را تعریف کرد. در همان اوقات که گالیله نخستین دوربین نجومی خود را به سوی آسمان متوجه کرد در 31 مارس 1596 در تورن فرانسه رنه دکارت به دنیا آمد. نام ریاضیدان بزرگ سوئیسی «پوب گولدن» را نیز باید با نهایت افتخار ذکر کرد.

[بزرگ‌نمایی تصویر]
شهرت وی بواسطه قضایای مربوط به اجسام دوار است که نام او را دارا می باشد و در کتابی به نام مرکزثقل ذکر شده. دیگر از دانشمندان برجسته قرن هفدهم پی یر دوفرما ریاضیدان بزرگ فرانسوی است که یکی از برجسته ترین آثار او تئوری اعداد است که وی کاملاً بوجود آورنده آن می باشد. ریاضیدان بزرگ دیگری که در این قرن به خوبی درخشید ژیرارد زارک فرانسوی است که بیشتر به واسطه کارهای درخشانش در هنر معماری شهرت یافت و بالاخره ریاضی دان دیگر فرانسوی یعنی روبروال که بواسطه ترازوی مشهوری که نام او را همراه دارد همه جا معروف است.
در اواسط قرن هفدهم کم کم مقدمات اولیه آنالیز عناصر بی نهایت کوچک در تاریکی و ابهام به وجود آمد و رفته رفته سر و صدای آن به گوش مردم رسید. بدون شک پاسکال همراه با دکارت و فرما یکی از سه ریاضیدان بزرگ نیمه اول قرن هفدهم بود و نیز می توان ارزش او را در علم فیزیک برابر گالیله دانست.
در نیمه دوم قرن هفدهم ریاضی بطور دقیق دنبال شد. سه نابغه فنا ناپذیر این دوره یعنی نیوتن انگلیسی، لایب نیتس آلمانی و هویگنس هلندی جهان علم را روشن کرده بودند. لایب نیتس در سال 1684 با انتشار مقاله ای درباره حساب عناصر بی نهایت کوچک انقلابی برپا کرد. هوگنس نیز در تکمیل دینامیک و مکانیک استدلالی با نیوتن همکاری کرد و عملیات مختلف آنها باعث شد که ارزش واقعی حساب انتگرال در توسعه علوم دقیقه روشن شود.
در قرن هجدهم دیگر تمام طوفانهای قرن هفدهم فرو نشست و تحولات این قرن عجیب به یک دوره آرامش مبدل گردید. دالامبر فرانسوی آنالیز ریاضی را در مکانیک به کار برد و از روشهای آن استفاده کرد. کلرو رقیب او در 18 سالگی کتابی به نام تفحصات درباره منحنی های دو انحنایی انتشار داد و در مدت شانزده سال رساله ای تهیه و به آکادمی علوم تقدیم نمود که شامل مطالب قابل توجهی مخصوصاً در مورد مکانیک آسمانی و هندسه بی نهایت کوچکها بود. دیگر لئونارد اویلر ریاضیدان بزرگ سوئیسی است که در 15 آوریل 1707 م. در شهر بال متولد شد و در 17 سپتامبر 1783 م. در روسیه درگذشت.
لاگرانژ از جمله بزرگترین ریاضیدانان تمام ادوار تاریخ بشر است. مکانیک تحلیلی او که در سال 1788 . عمومیت یافت بزرگترین شاهکار وی به شمار می رود. لاپلاس که در تدریس ریاضی دانشسرای عالی پاریس معاون لاگرانژ بود کتابی تحت عنوان مکانیک آسمانی در پنج جلد انتشار داد. گاسپار مونژ این نابغه دانشمند وقتی که هنوز بیست سال نداشت شاخه جدید علم هندسه به نام هندسه ترسیمی را بوجود آورد.
ژان باتیست فوریه در مسأله انتشار حرارت روش بدیع و جالبی اختراع کرد که یکی از مهمترین مباحث آنالیز ریاضی گردید. از دیگر دانشمندان بزرگ این قرن سیمون دنی پوآسون (1840-1781) فرانسوی و شاگرد لاپلاس می باشد که اکتشافات مهمی در ریاضیات نمود گائوس ریاضیدان شهیر آلمانی تئوری کامل مغناطیس را بوجود آورد. مطالعات او درباره انحناء و ترسیم نقشه ها و نمایش سطوح بر صفحات اصلی و اساسی می باشد.
کوشی فرانسوی که در سراسر نیمه اول قرن پانزدهم بر دیگر هموطنان برتری داشت با منطق دقیق خود تئوری های زیادی از حساب انتگرال را توسعه داد. آبل در سال 1824 ثابت نمود که صرفنظر از معادلات درجه اول تا درجه چهارم هیچ دستور جبری که بتواند معادله درجه پنجم را به نتیجه برساند وجود ندارد. گالوا که در 26 اکتبر 1811 م. در پاریس متولد شد تئوری گروهها را که قبلاً بوسیله کوشی و لاگرانژ مطالعه شده بود در معادلات جبری به کار برد و گروه جانشینی هر معادله را مشخص کرد.
دیگر از دانشمندان بزرگ این قرن ژنرال پونسله فرانسوی می باشد که آثاری همچون «موارد استعمال آنالیز در ریاضی» و «خواص تصویری اشکال» دارد همچنین لازار کانو فرانسوی که اکتشافات هندسی او دارای اهمیت فوق العاده می باشد. میشل شال هندسه مطلق را با بالاترین درجه استادی به بالاترین حد ممکن ترقی داد. در نیمه اول قرن نوزدهم ریاضیدان روسی نیکلاس ایوانویچ لوباچوشکی نخستین کشف خود را درباره هندسه غیراقلیدسی به جامعه ریاضیات و فیزیک قازان تقدیم کرد.
ادوارد کومرنیز در نتیجه اختراع نوعی از اعداد به نام اعداد ایده آل جایزه ریاضیات آکادمی علوم پاریس را از آن خود کرد. در اینجا ذکر نام دانشمندانی نظیر شارل وایرشتراس و شارل هرمیت که در مورد توابع بیضوی کشفیات مهمی نمودند ضروری است. ژرژ کانتور ریاضیدان آلمانی مکه در روسیه تولد یافته بود در ربع آخر قرن نوزدهم با وضع فرضیه مجموعه ها اساس هندسه اقلیدسی را در هم کوفت.
? کانتور مجموعه را به دو صورت زیر تعریف کرد:
1) اجتماع اشیایی که دارای صفت ممیزه مشترک باشند هر یک از آن اشیاء را عنصر مجموعه می گویند.
2) اجتماع اشیایی مشخص و متمایز
ولی ابتکاری و تصوری هنری پوانکاره یا غول فکر ریاضی آخرین دانشمند جهانی است که به همه علوم واقف بود. وی در بیست و هفت سالگی بزرگترین اکتشاف خود یعنی توابع فوشین را به دنیای دانش تقدیم نمود. بعد از پوانکاره ریاضیدان سوئدی متیاگ لفلر کارهای او را ادامه داد و سپس ریاضیدان نامی فرانسوی امیل پیکارد در این راه قدم نهاد. در اواخر قرن نوزدهم علم فیزیک ریاضی به منتها درجه تکامل خود رسید و دانش نجوم مکانیک آسمانی تکمیل گردید. امروزه ریاضیات بیش از پیش در حریم سایر علوم نفوذ کرده و نه فقط علوم نجوم و فیزیک و شیمی تحت انضباط آن درآمده اند بلکه اصولاً ریاضیات دانش مطلق و روح علم شده است.

منبع:

سازمان آموزش و پرورش استان خراسان

اشکال مرموز کشتزارهای گندم و هندسه دوجینی





دوایر مرموز :







حدودا بیست سال است که هر چند یک بار در یکی از کشورهای اروپایی واقعه عجیبی اتفاق می‌افتد . داستان هم این است که شب می‌خوابند و صبح که بیدار میشوند می‌بینند که در مزارع گندم دایره‌های بزرگی ایجاد شده است . این اتفاق نمی‌تواند عادی و یا شوخی و جعلی باشد . گذشته از این یک شبه نمی‌شود چنین اشکالی را با آن دقت در مزارع ایجاد کرد . در این بین بحران دایره‌های گندمزاری متوقف نشده است ، بلکه توسعه نیز یافته و جالب است که اشکال هندسی ، سال به سال هندسی‌تر ، پیچیده‌تر و پرکارتر شده‌اند .

ژاپنی‌ها موضوع را آنقدر جدی تلقی کرده‌اند که هیات‌هایی را برای بازدید از این دایره‌ها به اروپا و آمریکا فرستادند . نظر نهایی اینست که این اشکال ثمره هنرنمایی موجودات فضایی باهوشی است که سوار بر بشقاب پرنده به زمین می‌آیند و بوسیله اشکال مرموز برای ما پیغام می‌گذارند و دوباره به سیاره خود بر می‌گردند .

آزمایشها و بررسی‌های شبانه با کمک دوربینهای مادون قرمز و میکروفن‌ها ثابت کرده‌اند که این اشکال عجیب و غریب و شاید در باطن پر معنی ، شب هنگام و در کوتاه‌ترین زمان و بدون ایجاد کمترین سر و صدایی یا تظاهرات عینی و گویی که بطور صد در صد نامریی بوجود آمده‌اند .

این اشکال در طول 20 سال گذشته هندسی‌تر ، هنری‌تر ، پیچیده‌تر و پر طرح‌تر شده‌اند . مثلا دایره‌ها بزرگتر شده‌اند . گاهی دایره‌ها مانند حلقه‌های سمبل المپیک تو در تو هستند و در یک مورد هم یک مثلث نیز به آنها اضافه شده است . اشکالی هم شبیه حشرات و ماهی‌ها عینا مانند آثار نقاشی ماقبل تاریخ که در غارها کشف شده‌ دیده شده‌اند . در کل کسی که این اشکال را ایجاد کرده است در نوعی خط تصویری نظیر خط هیروگلیف مهارت داشته و خواسته است که با زبان بی زبانی به ما چیزهایی بگوید .

برخی از محققینی که ماجرا را مورد بررسی قرار داده‌اند ، می‌گویند که این اشکال از فضا و با کمک نوعی اشعه شبیه اشعه لیزر دایره‌وار سوزانده می‌شوند و بعید نیست که در حین عمل ، صدای خش و خش مانندی نیز بلند شده باشد . ولی در کل از روی شکل‌های این مزارع باید نتیجه گرفت که فاعل هر کسی که باشد ، روحیه اعتدالی دارد و از هندسه و هنر چیزهایی سرش می‌شود و در ضمن با طبیعت هم سر و کار دارد . بطور کلی می‌توان گفت که آنها موجودات بی آزار و صلح جویی هستند و می‌خواهند ، خود را به نحوی از انحا با طبیعت زمین تطبیق دهند و به ما حالی کنند که ما هم هستیم .

نیرویی که بتواند ساقه‌های گندم را خم کند ، الزاما باید ویژگیهای خاصی نیز داشته باشد . چون در بعضی از گندمزارها ساقه‌های گندم در این اشکال بریده و یا سوزانده نشده‌اند ، بلکه خیلی تمیز و پاکیزه با زاویه 90 درجه خم و خوابانده شده‌اند . یعنی به بوته گندم امکان داده شده است که به رشد خود ادامه دهد ولی نه بصورت قائم ، بلکه بصورت افقی .











مسئله کشف و تشخیص آثار رادیواکتیو در این اشکال ، موضوع را پیچیده تر کرده است . در تمام اشکال ، آثار تشعشعات رادیو اکتیو بتا و گاما ( البته با شدت ضعفهای متفاوت ) تشخیص داده شده است و آزمایشگاه‌ها نظر داده‌اند که در بعضی از مزارع ، مقدار اشعه بتا و گاما زیاد و در برخی کم است .

تشکیلات موسوم به حلقه‌های کشتزار ، اغلب در مزارع غلات پدید می‌آیند و طی فرآیندی که به پیدایش آنها می‌انجامد ، گیاهان به نحوی اسرار آمیز بر روی زمین می‌خوابند . بدین صورت الگو‌هایی پدید می‌آید که یک باره و بی آنکه در روشنایی روز پیش از آن ، کسی آنها را دیده باشد ، توجه مردم را به خود جلب می‌کنند .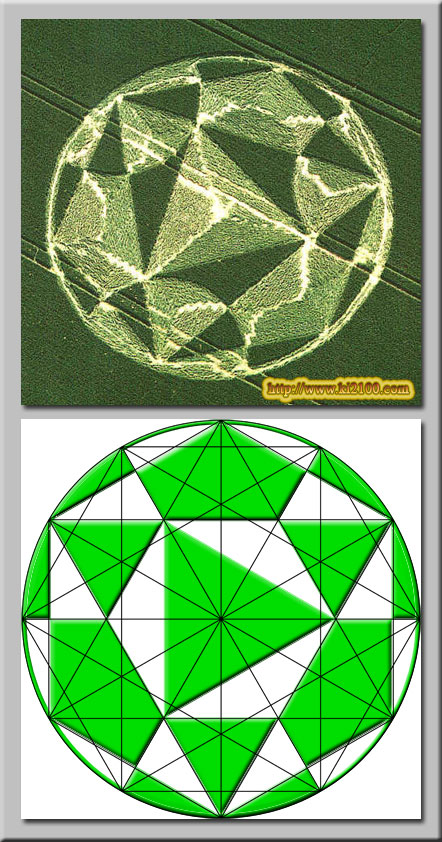







شواهد موجود نشان می‌دهند که وقوع این پدیده‌ها ، از اوایل قرن بیستم به بعد ، سال به سال افزایش یافته است ، به طوری که در دهه 1960 به رویدادی آشنا تبدیل شده و از دهه 1970 به بعد توجه اذهان عمومی را به خود جلب نموده است . از سال 1972به بعد ( یعنی سال مشاهده عینی صحنه وقوع توسط باند و شاتل وود ) تاکنون در حدود ده هزار گزارش از پیدایش مستند حلقه‌های کشتزار با اشکال گوناگون ، در نقاط مختلف جهان ارائه شده است . قطر بعضی از این حلقه‌ها به یک کیلومتر می‌رسد و برخی دیگر از آنها مساحتی بالغ بر 19 هزار متر مربع را می پوشانند .







در این تصویر ، صورت یک موجود نقش بسته است !



نکته جالب و شگفت انگیز دیگری که در این باره وجود دارد ، مسئله تحول و تکامل تدریجی این طرح‌ها میباشد . امروزه شاهد پدیدار شدن نگاره‌های هندسی بغرنجی هستیم که از روابط ریاضی پیچیده‌ای پیروی می‌کنند و جالب آنکه در برخی موارد ، این نگاره‌ها ، نمایانگر نقوش و طرح‌های مقدس اقوام و ملل مختلفی از سراسر جهان هستند .







نکته قابل ذکر دیگر ، نحوه خمیده شدن ساقه‌ها و ارتباط آن با ساختمان آنهاست . ساقه گیاهان علفی ، بندها یا گره‌هایی دارند که از وظایف آنها ، ایجاد استحکام در گیاه است . این بندها ، مجهز به روزنه‌هایی برای ایجاد امکان خروج بخار آب هستند . تجمع آب در محل بندها و فشار آن ، موجب راست ایستادن ساقه و در نتیجه ، موجب سر پا ماندن گیاه می‌شود . در صورتی که دما افزایش یابد ، آب به بخار تبدیل می‌شود و منافذ موجود در بندها ، راه را برای خروج بخار می‌گشایند . این ساز و کار ، راهی برای تنظیم دما و خنک نگه داشتن گیاه است ، که البته به از دست رفتن عامل استحکام و خمیده شدن ساقه گیاه می‌انجامد .










بررسی‌های میکروسکوپی نشان داده است که به هنگام پیدایش حلقه‌های کشتزار ، دقیقا همین عامل است که به خوابیدن رستنی‌ها بر روی زمین می‌انجامد . در واقع ، چنین به نظر می‌رسد که نوعی عامل خارجی باعث می‌شود در ناحیه بندها ، دما افزایش یابد . البته این خوابیدن برای رستنی‌های خشک شده و آماده درو نیز گزارش شده است .

نکته شگفت انگیز دیگر اینکه اثر این عامل خارجی ، انتخابی است . یعنی بندهایی که تحت تاثیر قرار می‌گیرند و جهت و میزان خمیدگی آنها ، بسته به طرحی که پیاده می‌شوند ، در بخش‌های مختلف تغییر می‌کند . مثلا ممکن است در یک سمت الگو ، نخستین بندهای بالاتر از سطح زمین ، آب از دست بدهند و در سمت دیگر ، دومین بندها . به این ترتیب ، به راحتی می‌توان آثار تقلبی را از نمونه‌های اصلی تشخیص داد . خم کردن ساقه‌ها با دست یا هر وسیله مکانیکی دیگری ، علاوه بر ایجاد آسیب در گیاه ، منجر به بروز خمیدگی‌هایی می‌شود که عمدتا در میان فواصل بندها و نه در خود آنها به وجود می‌آیند .

ساز و کار فوق نشان می‌دهد که احتمالا تابش امواجی نظیر مایکروویو که به صورت منفرد بر برخی از بندها اثر می‌کند ، عامل پیدایش الگوی خمیدگی هاست . با توجه به پیچیدگی هندسی طرح‌ها ، چنین می‌نماید که نوعی وسیله هدایت کننده اصلی ( نظیر یک رایانه ) فرمان‌های مقدماتی را به یک دستگاه عمل کننده نهایی ( نظیر دستگاه مولد پرتوها ) می‌فرستد و این دستگاه دوم ، اثر قابل مشاهده را بر بندهای ساقه اعمال می‌کند .

بررسی خاک مزارع در بخش داخلی طرح‌های مربوط به حلقه‌های کشتزار ، توسط دانشمندی به نام کالین اندروز ، نشان داده است که میزان تشعشع الکترومغناطیسی آن ، تا 100 ? بیشتر از حد عادی است و گزارش‌های ارائه شده ، مشخص کرده‌اند که در سالهای متعاقب این رویداد ، منطقه تحت تاثیر ، تا 40 ? با افزایش محصول رو به رو شده است .

همچنین ، اندازه‌گیری‌های مربوط به گسیل انرژی ، آشکار ساخته‌اند که تا چندین روز پس از پیدایش حلقه‌ها ، نوعی انرژی در محدوده فرکانس 5 کیلو هرتز ، از منطقه ساطع می‌شود که برخی از افراد حساس ، آن را در قالب صدایی لرزان می‌شنوند .

بسیاری از کسانی که از این حلقه‌ها بازدید می‌کنند ، دچار واکنش‌های جسمی خاصی می‌شوند که از آن جمله می‌توان به حالت تهوع ، سردرد ، گیجی ، احساس قلقلک و دردهای گوناگون اشاره کرد . نظیر این نشانگان را می توان در ناخوشی‌های حاصل از تاثیر پرتو رادیو اکتیو نیز مشاهده کرد .

گفته می‌شود که ساعت‌ها ، تلفن‌های همراه ، دوربین‌های عکاسی و به ویژه دستگاههای الکترونیکی که برای بررسی وارد منطقه می‌شوند ، دچار اختلال می‌شوند و نیز ادعا می‌شود که قطب نمای هواپیماها ، در بالای این مناطق ، به صورت دیوانه وار به چرخش در‌می‌آید .

اشخاصی که شاهد پیدایش حلقه‌های کشتزار بوده‌اند ، متوجه تابش سرخ رنگی بر سطح زمین شده‌اند . خمیده شدن گیاهان در 5 دقیقه اتفاق می‌افتد و در این مدت ، هیچ کس ، شخص یا وسیله‌ای را که بتوان این رویداد را به آن نسبت داد ، ندیده است .

در برخی موارد ، پیدایش اشکال پیچیده این حلقه‌ها با برخی حوادث عجیب همراه بوده است . مثلا دیده شده است که سگ‌های مجاور یک منطقه در فاصله ساعت 2 تا 4 بامداد پارس کرده‌اند و صبح روز بعد ، پیدایش حلقه‌ای در آن منطقه گزارش شده است ، و یا دیده‌اند که احشام ، پس از ورود به محوطه حلقه‌ها بیمار شده‌اند . در دامنه تپه‌ها ، متوجه وزش بادهای عجیب شده‌اند و همچنین مشاهده گوی‌های نارنجی نورانی ، شنیدن صداهای خش خش مانند عجیب و ظهور مکرر اشیاء پرنده ناشناس ، از دیگر وقایع پس از ظهور حلقه‌ها بوده‌اند .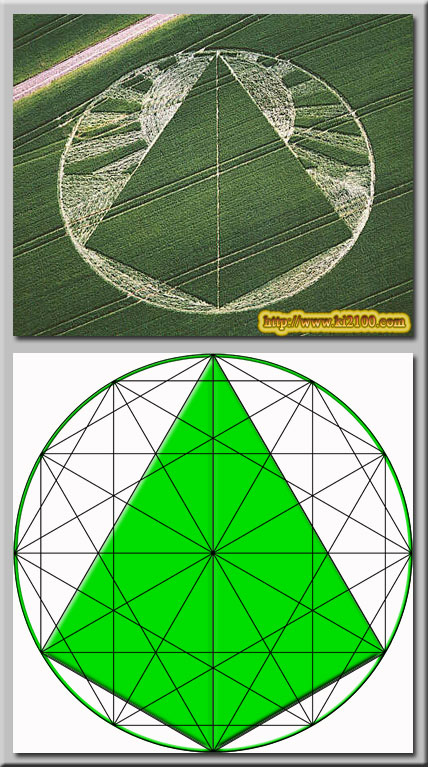







این تصویر عینا بر روی پلاک همسر توت ان خامون فرعون مصر نقش بسته بود و موجب تعجب دانشمندان گردیده است ! این تصویر عینا در اهرام مصر باستان وجود دارد ! این تصاویر و اشکال هندسی دلیلی بر اثبات وجود رابطه‌ای مابین فراعنه مصر و سرنشینان یوفو میباشد .


مشهورترین تصویر قدیمی مستندی که وقوع پدیده حلقه‌های کشتزار را نشان میدهد ، یک گراور یا حکاکی چوبی ، متعلق به سال 1678 میلادی در انگلستان است . در این اثر ، موجودی شیطانی به تصویر در آمده است که با داسی بلند ، مشغول دروی مزرعه غلات در قالب الگویی عجیب و خاص است .








این تصویر در سال 1992 ایجاد شده است . اگر دقت کنید عین همین تصویر در آثار باستانی اینکاها در امریکا دیده می‌شود . واقعا باور نکردنی است ! طول این تصویر 130متر و عرض آن 40 متر است ! مکان در گراسدورف آلمان میباشد . این تصاویر و اشکال هندسی دلیلی بر اثبات وجود رابطه‌ای مابین سرخ پوستان امریکا و سرنشینان یوفو میباشد .





توجیه اشکال هندسی در گندم‌زارها :



همانطور که در مورد ریاضیات مختص فیزیک توضیح داده شد ، مقوله ریاضیات برای انسان ، از شمارش موجودات هستی شروع شده و سیستم شمارش اعداد به تعداد انگشتان دو دست بوده است ( یعنی مبنای دهدهی ) ، در واقع راهبرد انسان در ریاضیات مقایسه تعداد اشیا با تعداد انگشتان دو دست است . یعنی یک حرفه دستی که امروزه مکانیزه و ماشینی شده است . در طول تاریخ ثبت شده که پیشرفت جامعه‌های متمدن با توسعه سیستم شمارش اعداد و نوشتار متن گفتار ( کتابت و کتاب نویسی ) همراه بوده که چنین به‌نظر میرسد که همگی ریشه در وحی کتب آسمانی و تاریخ ادیان داشته است . نشانه‌هایی از سیستم‌هایی از اعداد بر پایه سه ، چهار ، پنج ، شش ، هشت و بیست در میان سرخ پوستان آمریکای شمالی پیدا شده است . بعضی شواهد از سیستم اعداد بر پایه دوازده را میتوان در مثال اینکه هر فوت دوازده اینچ است یا هر شیلینگ انگلیسی دوازده پنس و یا اینکه هر سال دوازده ماه است و یا شبانه روز دو تا 12 ساعت است و ... ، ملاحظه کرد . اما در جوامع امروزی به‌نظر می‌رسد که سیستم اعداد بر پایه ده برنده شده است . البته نه به‌علت وجود مزایای ذاتی ، بلکه به نظر می‌رسد که به سبب وجود ده انگشت دو دست می‌باشد . اما با تحقیق و مطالعه متوجه این موضوع میشویم که سیستم شمارش اعداد بر مبنای 12 بر عالم حاکم شده است و این مسئله مربوط به خلقت خداوند میشود که دلیل آن در دو مبحث نظریه حبابهای سطحی و شالوده هندسه دوجینی ، نظریه ذرات حجمی و تردید در تئوری نیروی هسته‌ای قوی توضیح داده شد . سیستم دوجینی از بعضی جهات راحت‌تر از سیستم دهدهی است . راحتی فوق اصولا از این حقیقت ناشی میشود که تعداد مقسوم علیه‌های دوازده از تعداد مقسوم علیه‌های ده بیشتر میباشد . دوازده بر یک ، دو ، سه ، چهار ، شش و دوازده بخش‌پذیر است . بنابراین بسیاری از محاسبات دستی در سیستم دوجینی تا حدودی ساده‌تر از سیستم دهدهی هستند ، بعضی از کسرهای معمولی که در مبنای دهدهی به صورت عددهای کسری متناوب در می‌آیند در مبنای دوجینی چنین نیستند . برای نمونه کسر 3/1 که همان 12/4 میباشد در مبنای دوجینی به صورت 0.4 است و ..... که در صورت علاقمندی مراجعه نمایید به مبحث ریاضیات مختص فیزیک چیست ؟

چنین به‌نظر میرسد ، موجودات هوشمند منجمله انسان و UFO و USO که توانایی انجام دادن عملیات و محاسبات ریاضی را دارند به‌طور ذاتی از سیستم‌های شمارش بر مبنای ده‌تایی و دوازده‌تایی بهره میجویند . به عکسهای زیر توجه نمایید .










دو عکس فوق مربوط به دو موجود دریایی است که در میان گذشتگان ما به پری دریایی شهرت یافته است اما نه به آن زیبایی که در داستانهای کودکانه ما آمده است . همانطور که مشخص است تعداد انگشتان آنها در دو دست ، همانند انسان ده عدد میباشد .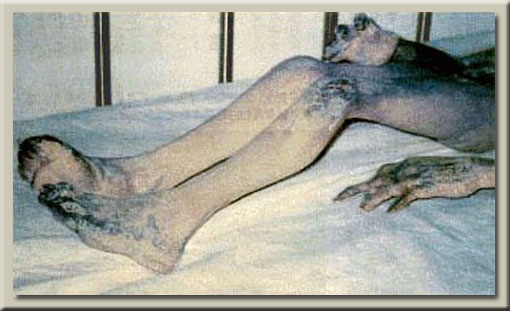







عکس فوق مربوط به جنازه یک سرنشین بشقاب پرنده است ( یوفو ) . همانطور که مشخص است تعداد انگشتان او در دو دست ، همانند انسان 10 عدد میباشد .






عکس فوق مربوط به ساخته دست یوفوها است ( اشیاء بدست آمده از سقوط بشقاب پرنده در واقعه روزول ) . همانطور که مشخص میباشد تعداد انگشتان سازنده آن 12 تا بوده است که بعضی از انسانها نیز به‌طور مادرزادی 12 انگشتی به دنیا می‌آیند . لازم به توضیح است که شواهد بسیاری دال بر وجود رابطه نزدیک مابین یوفوها و سرخ پوستان آمریکای شمالی ، حتی فراعنه مصر در دست است و با توجه به اینکه انسانها تاکنون از سیستم‌های شمارش متعددی غیر از ده استفاده نموده‌اند ، پیش بینی میشود که موجودات باشعوری با تعداد انگشتان متفاوتی نیز وجود داشته باشند ، منجمله عکس زیر .






عکسهای زیر مربوط به ترسیم‌هایی میشود که در قاره آمریکا روی زمین آنهم در ابعاد بزرگ کشف شده است و حاکی از مبناهای متعدد اعداد رایج در میان سرخ پوستان بوده است .





به هر حال تعداد انگشتان یک موجود هوشمند تاثیر زیادی در اندوخته‌های فکری و دانش او از عالم پیرامون دارد و چنین به‌نظر میرسد که موجودات 12 انگشتی باشعورترین ، موفق‌ترین و تکامل یافته‌ترین موجودات در عرصه علم و دانش منجمله ریاضیات و فیزیک باشند . و مسلما موجودات باهوش‌تری هم یافت میشوند که این سیستم شمارش اعداد را علی‌رغم مغایرت با تعداد انگشتان خود ، برگزیده‌اند چرا که نشانه‌هایی از آن سیستم در میان ما انسانها یافت میشود که دال بر وجود یک نوع رابطه علمی آنها با گذشتگان ما در روی سیاره زمین بوده است و شاید آنها با گذشتگان ما نوعی همزیستی داشته‌اند .







عکس فوق مربوط به جنازه یک موجود 12 انگشتی است که در کنار بشقاب پرنده سقوط کرده در نیومکزیکو ( واقعه روزول ) یافت شده است . اینک به رابطه این اشکال با سیستم شمارش دوجینی یا هندسه دوجینی میپردازیم و به چند نمونه از این اشکال گندم‌زار اشاره میکنیم .
















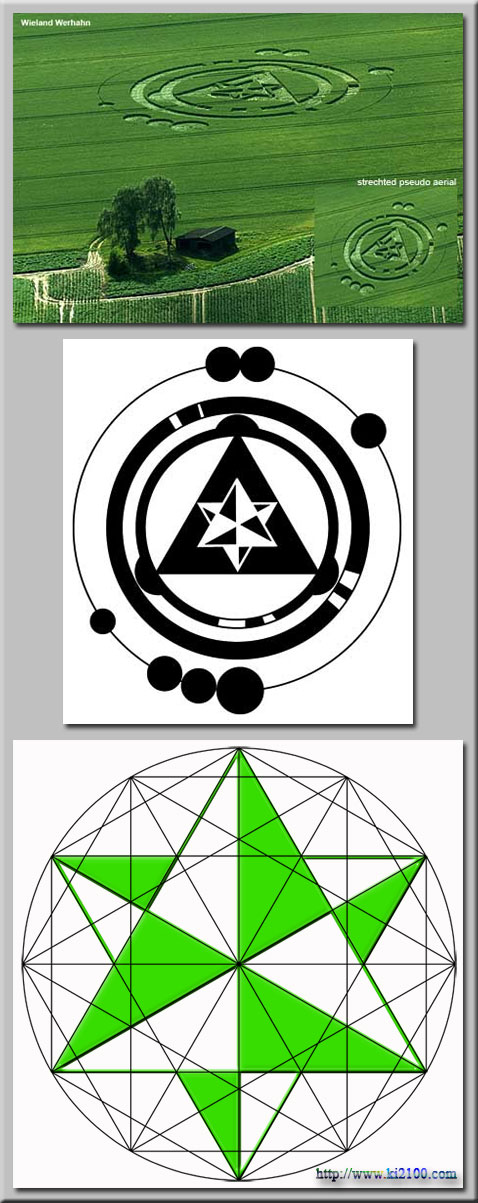
اشکال شش ضلعی برگرفته از ستاره داوود یعنی نمای ایزومتریک مکعب کاملا مشهود است . این اشکال ثابت می‌کند که سیستم شمارش اعداد و هندسه طراحان آن بر مبنای دوجینی است ، یعنی به تعداد انگشتان دو دستشان .


آلبوم تصاویر

منبع:محمدرضا طباطبایی