در مطلب جریان‌ تراکم‌پذیر عددی بی‌بعد تحت عنوان ماخ را معرفی کردیم. در بخش مذکور نشان دادیم که رابطه‌ای میان تراکم‌پذیری سیالِ در حال حرکت و عدد ماخ وجود دارد. در حقیقت در بخش‌های مختلفی از علوم، خصوصا فیزیک کلاسیک از اعدادی بی‌بعد استفاده می‌شود که می‌توان با استفاده از آن‌ها پدیده را توصیف کرد. در این مطلب قصد داریم تا  عددی بی‌بعد تحت عنوان «رینولدز» (Reynolds) را معرفی کنیم.

رینولدز عددی بی‌بعد در مکانیک سیالات است که الگوی جریان در حال حرکت را توصیف می‌کند. رینولدزِ اندک نشان‌دهنده جریان لایه‌ای و رینولدز بالا جریان «توربولانس» (Turbulence) را نشان می‌دهد. مفهوم کم و زیاد بودن عدد رینولدز را در ادامه بیان خواهیم کرد.

تعریف

عدد رینولدز نشان دهنده نسبت نیروهای اینرسی به نیروهای ویسکوز است که به دلیل حرکت سیال به وجود می‌آیند. از آنجایی که توربولانس و یا لایه‌ای بودن جریان وابسته به این نیرو‌ها است، از این رو با استفاده از عدد رینولدز می‌توان رژیم (لایه‌ای یا توربولانس بودن) یک جریان را تعیین کرد. اگر در یک سیال در حال حرکت، نیروهای اینرسی غالب باشند، به احتمال زیاد جریان مد نظر توربولانسی است. عکس این مورد، اگر نیروهای لزجت در یک سیال غالب باشند، سیال به صورت لایه‌ای حرکت می‌کند. با توجه به مفاهیم عنوان شده در بالا عدد رینولدز (Re) را می‌توان به صورت زیر تعریف کرد.

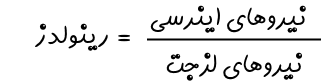
برای نمونه مطابق با شکل زیر لیوان آبی را در نظر بگیرید که به صورت ساکن قرار گرفته است. به این سیستم فقط نیروی گرانش وارد می‌شود. بنابراین صورت کسر رابطه بالا صفر است. در حالتی دیگر تصور کنید که لیوان را خالی کنیم. در این حالت با توجه به این‌که سیال در حال حرکت است، از این رو ذرات آن دارای تکانه هستند. در نتیجه نیرویی اینرسی در سیستم وجود دارد که منجر به غیرصفر شدن رینولدز می‌شود.

تاریخچه

نظریه استفاده از عدد بی‌بعد به‌منظور رصد کردن الگوی جریان، برای اولین بار توسط «جرج استوکس» (Sir George Stokes)، دانشمند ایرلندی ارائه شد. او در آزمایشی که می‌خواست نیروی درگ  را حول یک کره اندازه‌گیری کند، به این نتیجه رسید که با استفاده از عددی بی‌بعد می‌توان الگوی جریان عبوری روی آن را تعیین کرد. او با استفاده از مطالعاتی که توسط «ناویر» (Navier) انجام شده بود و با اضافه کردن عبارت‌های مرتبط با نیروی ویسکوز، توانست به معادلاتی برسد که انقلابی در فیزیک کلاسیک محسوب می‌شود.

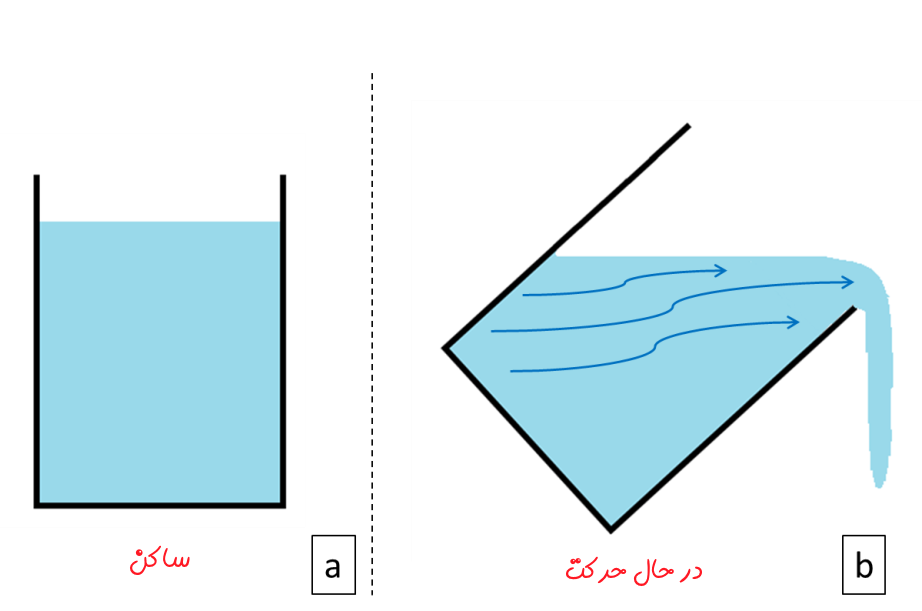
در سال 1883، رینولدز،‌ دانشمند ایرلندی عددی بی‌بعد را معرفی کرد که می‌توانست الگوی جریان را معلوم کند. او متوجه شد که این عدد به خواص استاتیکی و دینامیکی سیال، هم‌چون سرعت، چگالی، ویسکوزیته دینامیکی و … وابسته است. بنابراین آزمایشاتی را به‌منظور فهمیدن دقیق این رابطه انجام داد. برای این منظور سیستمی را مطابق با شکل زیر طراحی کرد. این سیستم به این صورت بود که لوله‌ای نازک که حاوی سیالی رنگی بود در یک لوله اصلی محتوی آب، قرار داده شد. سپس سیال رنگی درون آب به جریان در می‌آمد. بنابراین امکان دیدن حرکت سیال فرآهم می‌شد.

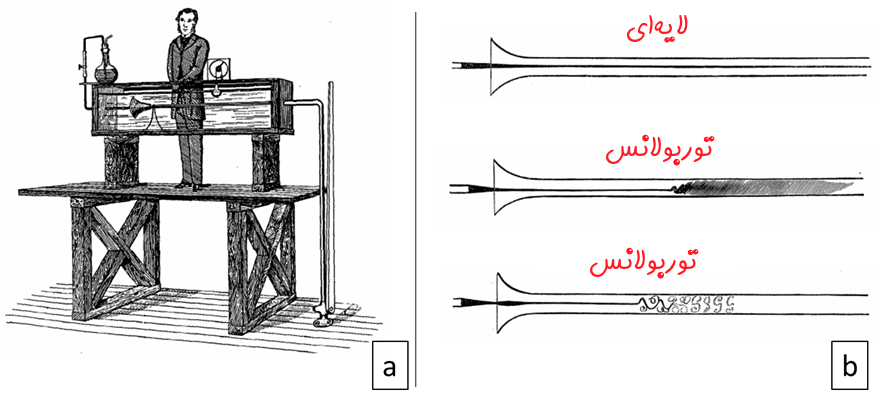
با توجه به آزمایش انجام شده، او توانست عددی بی‌بعد را تعریف کند که الگوی جریان وابسته به آن است.

استخراج عدد رینولدز

همان‌گونه که در بالا نیز بیان شد، با استفاده از این عدد می‌توان تعیین کرد که جریان با توجه به چه الگویی حرکت می‌کند. از آنجایی که این عدد نسبت نیروهای اینرسی به نیروهای برشی را نشان می‌دهند، بنابراین می‌توان گفت:

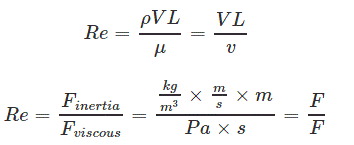
عبارت‌های استفاده شده در بالا به ترتیب زیر هستند:

• (ρ (kg/m³: چگالی سیال
• (V (m/s: سرعت سیال
• (L (m: طول مشخصه سیال
• (ν (m²/s: ویسکوزیته سینماتیکی سیال

همان‌طور که مشاهده می‌کنید با جایگذاری واحد‌های اجزا تشکیل دهنده عدد رینولدز، می‌بینید که این عدد، بی‌بعد است. البته در به دست آوردن رینولدز یک جریان می‌توان به جای ویسکوزیته سینماتیکی، با استفاده از تبدیل زیر از ویسکوزیته دینامیکی نیز بهره برد.

$$\nu =\frac{\mu }{\rho }$$

سیال، جریان و عدد رینولدز

روش محاسبه رینولدز با توجه به تراکم‌پذیر بودن سیال، تغییر پذیری ویسکوزیته (سیال غیرنیوتونی)، داخلی و یا خارجی بودن جریان متفاوت است. رینولدز بحرانی عددی است که در آن جریانِ سیال شروع به توربولانس شدن می‌کند. این مقدار در حالت‌های مختلفِ جریان، متفاوت است. به عنوان مثال برای جریانی که در لوله حرکت می‌کند، رینولدز بحرانیش برابر با 2300 است؛ یا این‌که برای حالتی که سیالی روی یک سطح تخت جریان دارد، مقدار رینولدز بحرانی بین 10⁵ تا 10⁶ است.

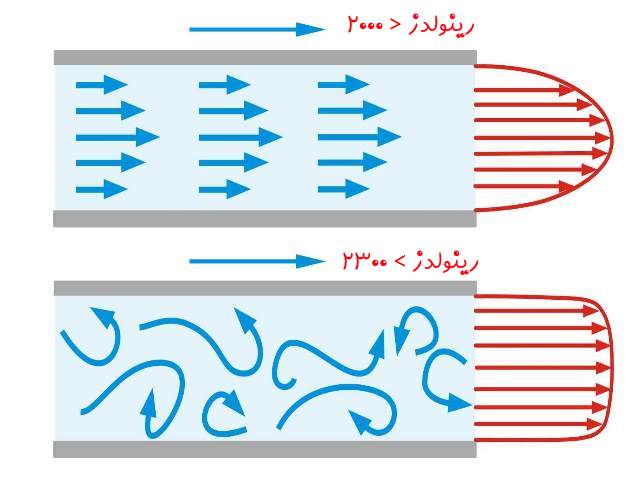
عدد رینولدز هم‌چنین می‌تواند توصیف دقیقی را از لزجت ارائه دهد. از این رو درک حالت سیال در هر لحظه بسیار مهم است. منظور از جمله قبل، این است که بدانیم جریان را به چه صورت بایستی فرض کرد. برای نمونه بدانیم که جریان داخلی، خارجی، گذرا و یا تراکم پذیر است؟ در هر یک از حالات ذکر شده مفهوم و حتی محاسبه عدد رینولدز معنای خاص خود را دارد. در ادامه به بررسی این عدد در سیالات نیوتنی می‌پردازیم. به سیالاتی نیوتنی گفته می‌شود که در آن‌ها رابطه میان تنش برشی و گرادیان سرعت به صورت خطی است. هم‌چنین در این سیالات ویسکوزیته ثابت است و تنها تابعی از دمای سیال است.

محاسبه رینولدز در حالت‌های مختلف

در حالت کلی رژیم جریان به دو دسته تقسیم‌بندی می‌شود: «لایه‌ای» (Laminar) و «توربولانس» (Turbulent). البته اگر بخواهیم درست‌تر بیان کنیم، حالت سومی نیز وجود دارد که به آن گذرا گفته می‌شود. این حالت زمانی اتفاق می‌افتد که بخشی از جریان به صورت لایه‌ای و بخشی دیگر به صورت توربولانس است.

جریان داخلی

به جریانی که درون لوله حرکت می‌کند، جریان داخلی می‌گویند. رینولدز‌های بحرانی برای چنین جریانی در جدول زیر بیان شده‌اند.

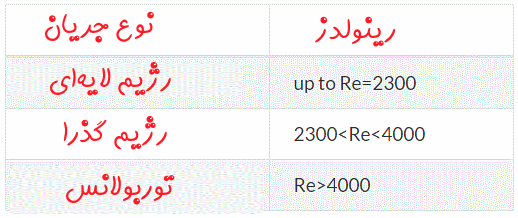
در حالتی که جریانی در یک کانال بسته و یا در لوله حرکت می‌کند، عدد رینولدز وابسته به قطر هیدرولیکی لوله (D_H) و طول آن (L) است. هم‌چنین در حالتی که لوله به صورت استوانه‌ای باشد، قطر هیدرولیکی آن در واقع همان قطر لوله است. بنابراین در این حالت عدد رینولدز به صورت زیر محاسبه می‌شود.

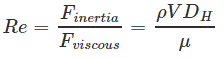
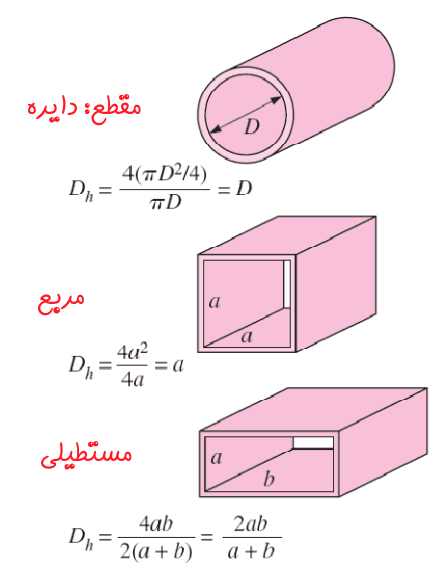
در حالتی که مقطع لوله به صورت دایره‌ای نباشد، می‌توان با استفاده از رابطه زیر قطر هیدرولیکی لوله را محاسبه کرد.

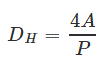
در معادله بالا A برابر با مساحت سطح مقطع لوله و P محیط تر شده است. در شکل‌های زیر قطر هیدرولیکی برای چند مقطع مختلف آورده شده‌اند.

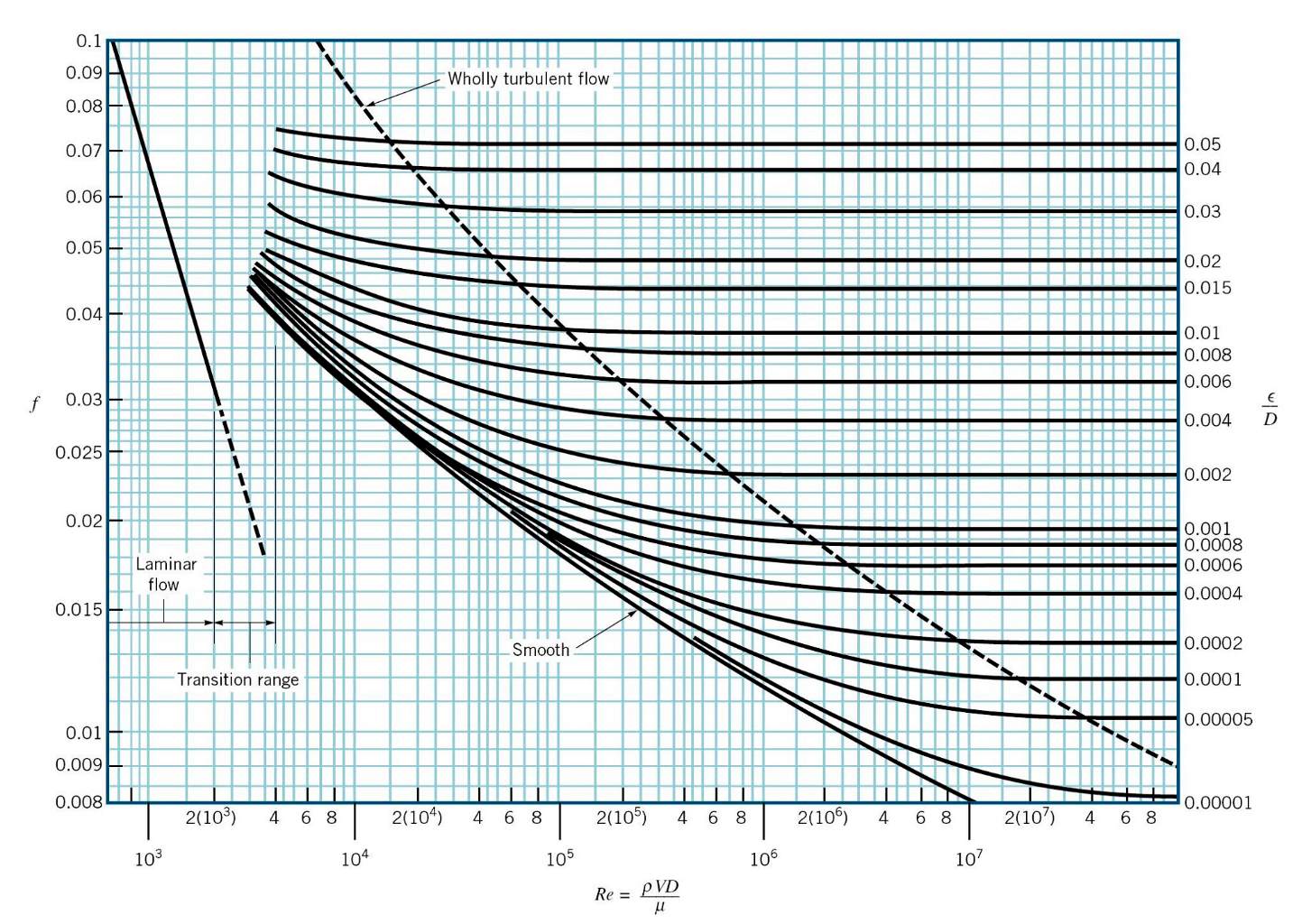
از دیگر عواملی که در توربولانس شدن جریان درون لوله موثر است، میزان اصطکاک سطح لوله با جریان خواهد بود. «نمودار مودی» (Moody Chart) میزان توربولانسی جریان را بر حسب عدد رینولدز و زبری سطحِ لوله، نشان می‌دهد. این نمودار روشی عملی به منظور محاسبه افت فشارِ جریان سیالی است که درون لوله حرکت می‌کند. اگر توجه داشته باشید در نمودار زیر ناحیه‌های توربولانس و لایه‌ای بر حسب ضریب اصطکاک و رینولدز جریان نشان داده شده‌اند.

جریان خارجی

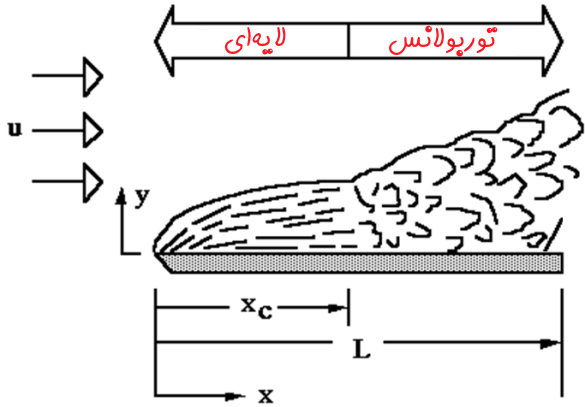
به جریانی که روی اجسام به حرکت در می‌آید، جریان خارجی گفته می‌شود. برای نمونه جریان روی یک صفحه تخت، جریان روی کره یا سیلندر همگی از نوع جریان‌های خارجی هستند. در سال 1914 «لودویگ پرانتل» (Ludwig Prandtl)، دانشمند آلمانی مفهوم لایه‌مرزی را ارائه کرد. او دریافت که لایه‌مرزی به رینولدز و شکل سطح وابسته است. در شکل زیر جریانی را روی سطحی تخت نشان می‌دهد. در نقطه x_c جریان شروع به توربولانس شدن می‌کند.

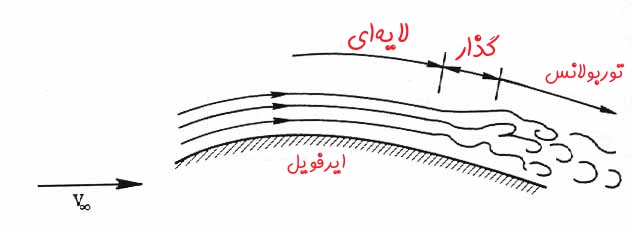
شکل زیر جریان خارجی را روی یک ایرفویل نشان می‌دهد. همان‌طور که می‌بینید این جریان در ابتدا لایه‌ای سپس گذرا و نهایتا به یک جریان توربولانس تبدیل شده است. دلیل این امر متفاوت بودن عدد رینولدز در هر کدام از این نقاط است.

در حالت کلی با حرکت جریان رو به جلو، سیال منبسط و البته ناپایدارتر می‌شود. این ناپایداری منجر به افزایش رینولدز شده و نهایتا توربولانس شدن جریان را در پی دارد. رینولدز بحرانی برای جریان روی سطح بایستی بیشتر از مقدار زیر باشد.

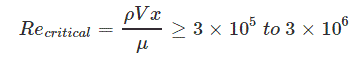
رینولدزهای بالا و پایین

در روش‌های عددی حل شده برای معادله ناویر-استوکس، عدد رینولدز نیز ظاهر می‌شود. شکل ساده شده معادله ناویر-استوکس که تحت عنوان معادله اویلر شناخته می‌شود، به صورت زیر است.

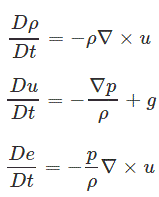
در معادله بالا ρ برابر با چگالی و u و p به ترتیب برابر با سرعت و فشار هستند؛ همچنین e نشان دهنده انرژی داخلی ویژه سیال است. توجه داشته باشید که اثرات لزجت در مدل‌سازی سیال بسیار مهم هستند. با این وجود در بعضی از موارد می‌توان از مدل سیال غیرلزج به‌منظور شبیه‌سازی سیال بهره برد. برای نمونه در حالت جریان خارجی با سرعت بالا، می‌توان معمولا از مدل سیال غیرلزج بهره برد.

از طرفی زمانی که Re?1 (بسیار بسیار کم‌تر از 1) باشد، اثرات اینرسی را می‌توان در معادله ناویر-استوکس حذف کرد. به ورژنی از معادله ناویر-استوکس که در رینلدز پایین نوشته می‌شود، جریان استوکس گفته می‌شود. بنابراین در حالتی که رینولدز جریان کم باشد،‌ معادله ناویر-استوکس به شکل زیر در می‌آید.

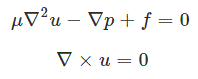
در معادله بالا u سرعت سیال، p∇ گرادیان فشار و μ لزجت سیال را نشان می‌دهند. از جریان استوکس می‌توان به منظور مدل‌سازی جریان ماگمای آتشفشانی، حرکت میکرو ارگانیز‌م‌ها و یا جریان پلمیر استفاده کرد.

کاربردهای عدد رینولدز

 تحلیل عددی جریان سیال، مبتنی بر مدل‌های ریاضیاتی ارائه شده است. شکل بی‌بعد شده این معادلات، اعداد بی‌بعد را نیز در دل خود خواهند داشت. این مدل‌ها با استفاده از آزمایش و قوانین بدست آمده‌اند. به‌منظور تحلیل عددی یک پدیده سیالاتی بایستی مدل ریاضیاتی را به نحوی انتخاب کرد که قابلیت مدل‌سازی دامنه حل را داشته باشد. در تمامی این مدل‌ سازی‌ها عدد رینولدز نقش به‌سزایی را در معادلات ایفا می‌کند. برای نمونه حرکت گلیسیرین را در لوله‌ای با مقطع دایره‌ای در نظر بگیرید. با فرض این‌که خواص سیال را داشته باشیم، می‌توان رژیم آن را به شکل زیر تعیین کرد.

در اولین قدم بایستی خواص سیال مفروض را داشته باشیم. جدول زیر این خاصیت‌ها را نشان می‌دهد.

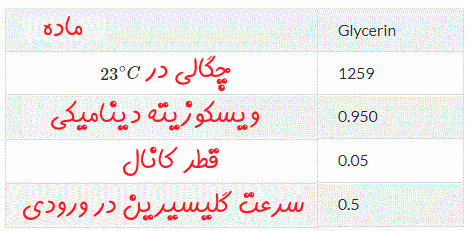
قدم بعدی، محاسبه رینولدز به شکل زیر است.

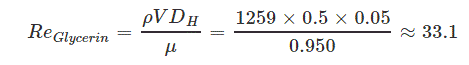
عدد بدست آمده کمتر از 2300 است، از این رو می‌توان این جریان را به صورت لایه‌ای در نظر گرفت.

این عدد مفهومی عمومی در مکانیک سیالات است که در بسیاری از مباحث مرتبط با حرکت سیال ظاهر خواهد شد.