انتگرال‌گیریِ جزء به جزء از روش‌هایی است که در محاسبه انتگرال توابعی که در یکدیگر ضرب شده‌اند، بسیار کاربرد دارد. در این مطلب در ابتدا فرمول انتگرال‌گیری جزء به جزء را بیان می‌کنیم. فارغ از این‌ که این فرمول برای شما گیج‌کننده باشد یا نه، باید بگوییم پس از حل چندین مثال که در ادامه آن آمده، حتماً این مفهوم را به خوبی هضم خواهید کرد.

محاسبه انتگرال به روش جزء به جزء

دو تابع (u(x و (v(x را فرض کنید. تصور کنید می‌خواهیم انتگرال تابع (u‘(x)v(x را بدست آوریم. انتگرال این تابع را می‌توان با استفاده از فرمول زیر محاسبه کرد.

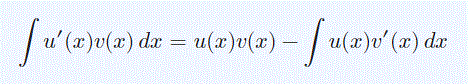
اجازه دهید هم‌چون فیلم‌های سینمایی به عقب برگردیم و داستان به‌دست آمدن این فرمول‌ را روایت کنیم. برای این منظور دو تابع (u(x و (v(x را فرض کنید. از مطلب ارائه شده در مورد مشتق می‌دانیم که مشتق تابع (u(x)v(x برابر با عبارت زیر است.

عبارتِ دومِ سمتِ راستِ معادله بالا را به سمت چپ منتقل می‌کنیم؛ با انجام این کار رابطه بالا به شکل زیر قابل بازنویسی است.

حال از طرفین این رابطه انتگرال می‌گیریم. همان‌طور که می‌دانیم، انتگرالِ مشتقِ یک تابع، برابر با خود تابع است. بنابراین می‌توان نوشت:

در نتیجه با انتگرال‌گیری از رابطه بالا به فرمول نهایی ارائه شده می‌رسیم.

بنابراین می‌توان گفت:

رابطه (*)

البته فرمول بالا را می‌توان با روشی آسان‌تر و به صورت زیر پیاده کرد.

رابطه (**)

بنابراین به منظور محاسبه یک انتگرال به روش جزء به جزء در ابتدا بایستی توابع f و g را به نحوی انتخاب کرد که انتگرال توابع f و g‘f قابل محاسبه باشند. سپس با جایگذاری این مقادیر در معادله بالا به راحتی انتگرال تابع fg بدست می‌آید.

مثال‌ها

شاید در ابتدا فرمول بالا کمی مشکل به نظر برسد. از این رو به شما پیشنهاد می‌کنیم تا مثال‌های زیر را مطالعه فرمایید. به یاد داشته باشید که مهم‌ترین قدم در محاسبه یک انتگرال، انتخاب مناسب توابع f و g هستند. برای نمونه فرض کنید بخشی از تابع زیر انتگرال از عبارت $\frac{sin\left(x\right)}{x}$

تشکیل شده. واضح است که اگر شما این تابع را به عنوان f در نظر بگیرید، دیگر امکان محاسبه F (که همان انتگرال f است) وجود نخواهد داشت.

مثال 1

حاصل انتگرال xe^x را بیابید.

فرض کنید می‌خواهیم با استفاده از رابطه ** این انتگرال را حل کنیم. با فرض کردن دو تابع x و e^x به عنوان g و f می‌توان نوشت:

مثال 3

پاسخ انتگرال تابع (xcos(x را با استفاده از روش جزء به جزء بدست آورید.

توجه داشته باشید که همواره f و g را به شکلی در نظر بگیرید، که امکان محاسبه انتگرال تابع g‘f وجود داشته باشد. البته تابع f را نیز بایستی به نحوی در نظر گرفت که بتوانیم انتگرال آن را محاسبه کنیم. در این مثال x و (cos(x را به ترتیب برابر با g و f در نظر می‌گیریم. از این رو با جایگذاری این دو تابع در فرمول ** داریم:

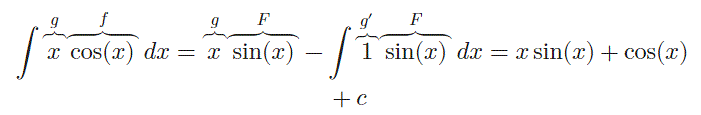
می‌توان در حالت کلی گفت که تابع ساده‌تر را بایستی به عنوان g در نظر گرفت. برای نمونه در این مثال x را به عنوان تابع g در نظر گرفته‌ایم. مثال 4 به درک بهتر انتخاب f و g کمک می‌کند.

مثال 4

حاصل عبارت $\int x\ln \left(x\right)dx,$

را بیابید.

در این مثال به نظر می‌رسد که اگر x را به عنوان f در نظر بگیریم، F که همان انتگرال f است، راحت‌تر محاسبه شده و انتگرال تابع g‘f را نیز می‌توان راحت‌تر یافت. از این رو x را برابر با f و (ln(x را برابر با g فرض می‌کنیم. بنابراین با توجه به فرض صورت گرفته می‌توان نوشت:

توجه داشته باشید که در بعضی از موارد ممکن است نیاز باشد با دو بار استفاده از روش جزء به جزء، حاصل انتگرال را بدست آورد. در مثال 5 نمونه‌ای از چنین مثالی آورده شده است.

مثال 5

پاسخ $\int x^2\sin \left(x\right)dx$

را بدست آورید.

همان‌طور که کمی بالاتر بیان کردیم، معمولا در محاسبه یک انتگرال به روش جزء به جزء بهتر است که تابع ساده‌تر را به عنوان g در نظر بگیریم. در نتیجه در این مثال تابع g را برابر با x² در نظر می‌گیریم؛ بنابراین (sin(x نیز معادل با f است. همانند مثال‌های قبلی با استفاده از فرمول ** داریم:

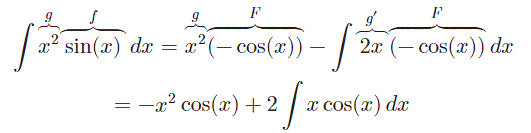
همان‌طور که می‌بینید برای محاسبه پاسخ این مثال به عبارت $\int x\cos \left(x\right)dx$

می‌رسیم. پاسخ این عبارت در مثال 3 محاسبه شد. از این رو با جایگذاری پاسخ مثال 3 در رابطه بالا، جواب نهایی به صورت زیر یافت می‌شود.

شاید با خود فکر کرده باشید که چرا به جای 2c از c استفاده کرده‌ایم. باید توجه داشته باشید که مشتق یک عدد ثابت همواره صفر است بنابراین هر مقدار ثابتی به جای c قرار گیرد، صحیح است.

حال وقت آن رسیده تا کمی خود را محک بزنید. مثال پیش‌رو اندکی دشوار‌تر از مثال‌های قبلی است.

مثال 6

انتگرال تابع $x\sqrt{x+1}$

را بیابید.

همان‌طور که بیان شد، در ابتدا تابع ساده‌تر را برابر با g در نظر بگیرید و چک کنید که آیا با این فرض، مسئله قابل حل است؟ بنابراین در این مثال تابع g را برابر با x و تابع f را برابر با $\sqrt{x+1}$

در نظر می‌گیریم. در بالا بیان کردیم که F همان انتگرال تابع f است. با توجه به مفاهیم ارائه شده در مطلب روش‌های محاسبه انتگرال، قانون توان در محاسبه یک انتگرال را به صورت زیر بیان کردیم:

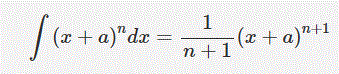
با استفاده از قانون توان، انتگرال تابع ${(x+1)}^{1/2}$

،‌ به شکل زیر محاسبه می‌شود.

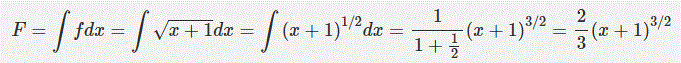
حال با بدست آمدن F می‌توان از فرمول ** به شکل زیر استفاده کرد.

مسلط شدن به این روش منوط به حل مثال است. در این روش نکته مهم انتخاب توابع f و g مناسب است.